21 相关性矩阵
21.1 什么是相关性矩阵?
相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度。相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。
当两个变量之间存在非常强烈的相互依赖关系的时候,我们就可以说两个变量之间存在高度相关性。若两组的值一起增大,我们称之为正相关,若一组的值增大时,另一组的值减小,我们称之为负相关。
默认一般使用皮尔逊算法算相关性。皮尔逊相关系数广泛用于度量两个变量之间的相关程度,其值介于-1与1之间。
计算完相关性后,我们通过相关性矩阵做可视化。矩阵的上下中三个面板支持多种图案,有热力图,柱形图,散点图,折线图,饼图等多种模式可供选择。
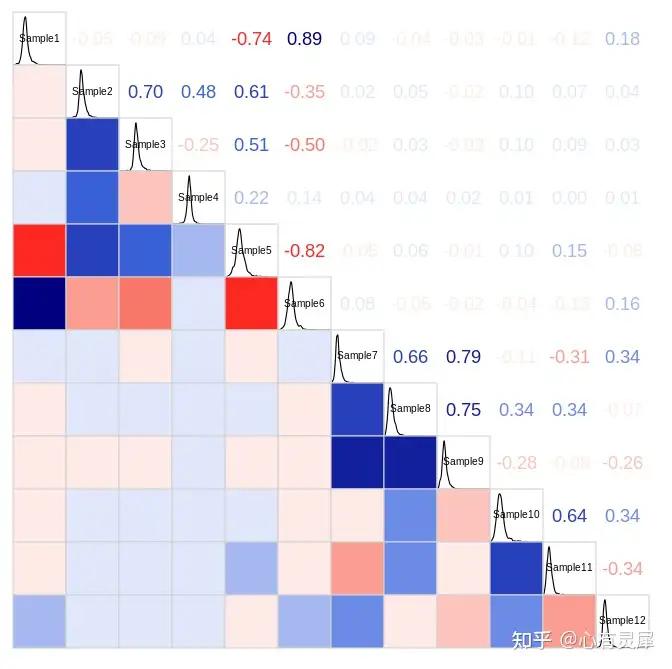
本文我们就来讨论一下相关性矩阵是如何绘制的以及如何对其进行解读。
21.2 绘图前的数据准备
demo数据可以在https://www.bioladder.cn/shiny/zyp/bioladder2/demoData/Cor/demo2.txt下载。
包含2个维度的数据,通常情况下每一行代表一个基因,每一列代表一个样本。

21.3 R语言怎么画相关性矩阵
# 加载R包,没有安装请先安装 install.packages("包名")
library(corrgram)
# 读取相关性矩阵数据文件
df= read.delim("https://www.bioladder.cn/shiny/zyp/bioladder2/demoData/Cor/demo2.txt",# 这里读取了网络上的demo数据,将此处换成你自己电脑里的文件
header = T,
row.names = 1
)
# 绘图
corrgram(df,
cex.labels = 0.8, # 样本文字大小
lower.panel="panel.pts", # 指定下方面板的形状,具体参数看下方注释
upper.panel="panel.cor", # 指定上方面板的形状,具体参数看下方注释
diag.panel="panel.density",# 指定中间面板的形状,具体参数看下方注释
cor.method="pearson") # 计算相关性的方法有"pearson", "spearman", "kendall"
# 上、下面板可供选择的图形
# "散点" = "panel.pts"
# "柱形" = "panel.bar"
# "相关系数(带置信区间)"="panel.conf"
# "相关系数(带颜色)"="panel.cor"
# "ellipse"="panel.ellipse"
# "填充"="panel.fill"
# "饼图"="panel.pie"
# "阴影"="panel.shade"
# "空"=NULL
# 中间面板可供选择的图形
# "核密度图" = "panel.density"
# "最大最小值" = "panel.minmax"
# "空"=NULL
# 更多参数可以输入 ?corrgram 查看21.4 相关性矩阵结果解读
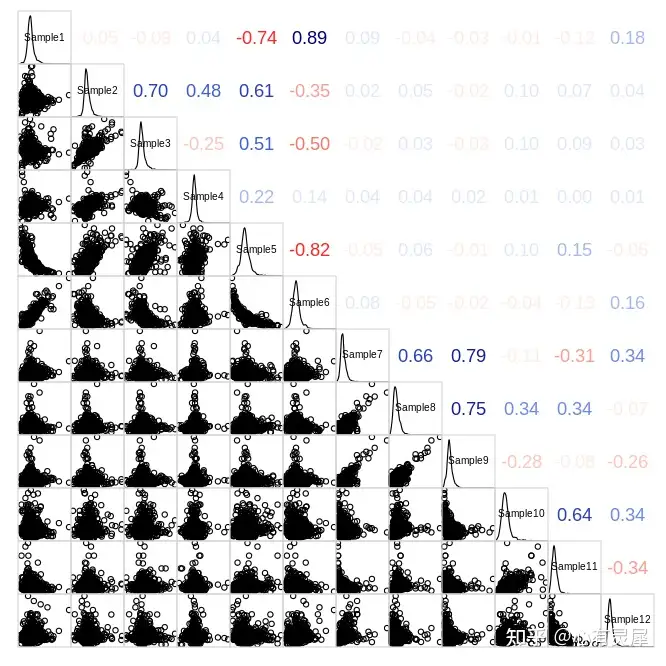
如示例结果所示,左面板采用的是散点图,如果散点图的形状接近一条直线,则相关性越好,若两组的值一起增大,我们称之为正相关,若一组的值增大时,另一组的值减小,我们称之为负相关,即”/“这种形状的为正相关,”\“这种形状的为负相关。中间的面板采用的是分布曲线+样本名称的方式。右面板采用的是相关性系数数字加上颜色深浅的方式来直观表达相关性的大小。
此外,面板还支持多种形状,散点图、柱状图、相关性系数大小、折线图、热图和饼状图等。当然也支持”无”,即此面板不放任何东西。
21.5 BioLadder生信云平台在线绘制相关性矩阵
不想写代码?可以用BioLadder生信云平台在线绘制相关性矩阵。
网址: