R语言如何绘制三维PCA图

前言

本文是R包plot3D绘制三维PCA的教程。

什么是PCA？

人眼一般能感知的空间为二维和三维。高维数据可视化的重要目标就是将高维数据呈现于二维或三维空间中。高维数据变换就是使用降维度的方法，使用线性或非线性变换把高维数据投影到低维空间，去掉冗余属性，但同时尽可能地保留高维空间的重要信息和特征。

PCA, 主成分分析法，也被称为主分量分析法，是很常用的一种数据降维方法。主成分分析法采用一个线性变换将数据变换到一个新的坐标系统，使得任何数据点投影到第一个坐标（第一主成分）的方差最大，在第二个坐标（第二主成分）的方差为第二大，以此类推。因此，主成分分析可以减少数据的维数，并保留对方差贡献最大的特征。

三维PCA和普通PCA的区别就是多了一个维度。

是主成分分析的PC1，PC2和PC3的结果，xyz坐标分别为前三个主成分，括号内的百分比为该主成分能解释的变量的百分比。PCA得分图能将对照组和实验组样本区分开。在PCA图中，如果样本之间聚集在一起，说明这些样本差异性小；反之样本之间距离越远，说明样本之间差异性越大。不同颜色的散点表示不同实验分组的样本。

绘图前的数据准备

绘图数据

数据来源一般是搜库结果定量表。包含2个维度的数据，一般情况下，每一行是一个基因，每一列是一个样本。

demo数据可以在https://www.r2omics.cn/res/demodata/PCA/data.txt下载。

分组数据

demo数据可以在https://www.r2omics.cn/res/demodata/PCA/sample.class.txt下载。

R语言如何绘制三维PCA图

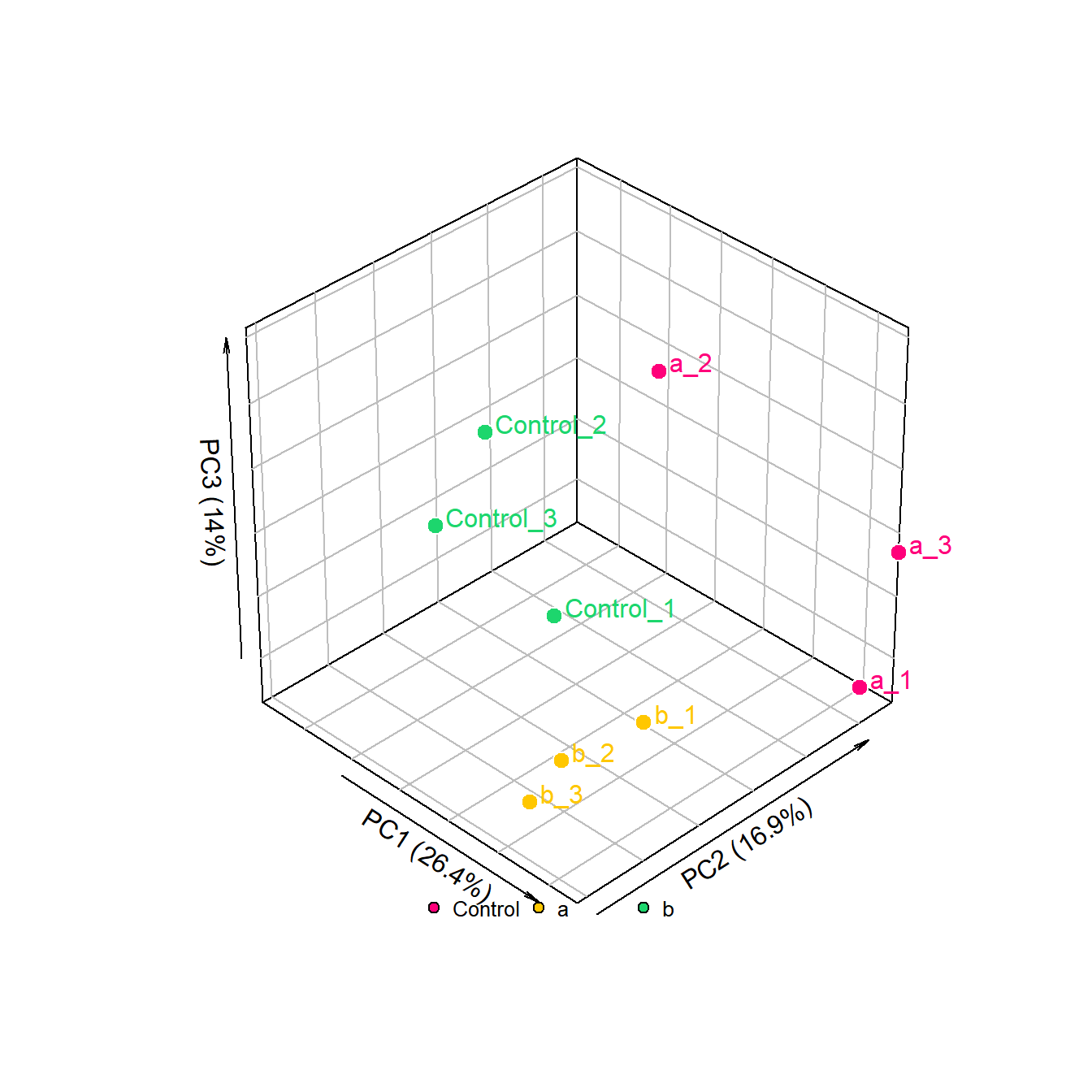
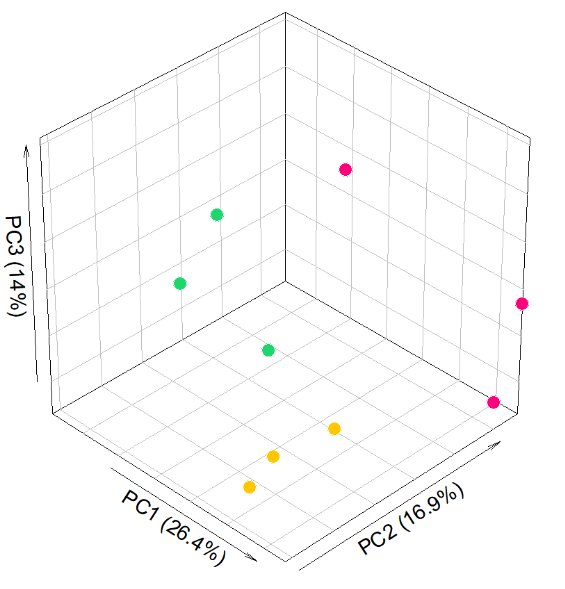
# 代码来源：https://www.r2omics.cn/
# 加载R包，没有安装请先安装  install.packages("包名")
library(plot3D)

# 读取PCA数据文件
df = read.delim("https://www.r2omics.cn/res/demodata/PCA/data.txt",# 这里读取了网络上的demo数据，将此处换成你自己电脑里的文件
                header = T,    # 指定第一行是列名
                row.names = 1  # 指定第一列是行名
)
df=t(df) # 对数据进行转置，如果想对基因分组则不用转置

# 读取样本分组数据文件
dfGroup = read.delim("https://www.r2omics.cn/res/demodata/PCA/sample.class.txt",
                     header = T,
                     row.names = 1
)

# PCA计算
pca_result <- prcomp(df,
                     scale=T  # 一个逻辑值，指示在进行分析之前是否应该将变量缩放到具有单位方差
)
pca_result$x<-data.frame(pca_result$x)

# 设置颜色，有几个分组就写几个颜色
colors <- c("#ff007a","#ffc700","#1dd66d")
myColors <- colors[as.numeric(as.factor(dfGroup[,1]))]


# 计算PC值，用来替换坐标轴上的标签
pVar <- pca_result$sdev^2/sum(pca_result$sdev^2)
pVar = round(pVar,digits = 3)
xName = paste0("PC1 (",as.character(pVar[1] * 100 ),"%)")
yName = paste0("PC2 (",as.character(pVar[2] * 100 ),"%)")
zName = paste0("PC3 (",as.character(pVar[3] * 100 ),"%)")

# 绘图
with(data.frame(pca_result$x[,1:3]), plot3D::scatter3D(
  x = PC1,       # 根据数据里的列名，设置X轴映射
  y = PC2,
  z = PC3,
  pch = 21,      # 设置散点的形状为实心圆
  cex = 1.5,     # 设置散点的大小
  col=NA,        
  bg=myColors,   # 设置散点的背景色
  xlab = xName,  # 设置 x 轴标签
  ylab = yName,
  zlab = zName,
  ticktype = "simple",  # 设置刻度线类型，还有detailed选项
  bty = "b2",    # 设置主题 b
  box = T,       # 显示坐标轴盒子
  theta = 45,    # 设置旋转角度
  phi = 35,      # 设置视角角度
  d=10,
  colkey = F     # 不显示颜色键
))

# 标签
legend("bottom",     # 指定图例位置在底部
       title = "",   # 设置图例标题为空
       legend = unique(dfGroup$Group),  # 使用数据框 dfGroup 中的组别进行标记
       pch = 21,     # 设置图例标记的形状为实心圆
       pt.cex = 1,   # 设置图例标记的大小
       cex = 0.8,    # 设置图例文本的大小
       pt.bg = colors,  # 设置图例标记的背景色
       bg = "white",  # 设置图例的背景色
       bty = "n",     # 去除图例的边框
       horiz = TRUE   # 设置图例水平显示
)

# 添加散点的文字标注
with(data.frame(pca_result$x[,1:3])+1,   # 在原来的数据上+1设置一个偏移量
  plot3D::text3D(
  x = PC1,       # 根据数据里的列名，设置X轴映射
  y = PC2,
  z = PC3,
  colkey = FALSE,
  add = TRUE,
  labels = row.names(pca_result$x),
  col = myColors))